对于一道高中数学题的讨论（虽然题目很简单）

骑驴赏月

题目

1.求函数 f(x)=\frac{x}{x+1}+\frac{x+1}{x+2} 图像的对称中心坐标。
2.求函数 f(x)=\frac{x}{x+1}+\frac{x+1}{x+2}+\frac{x+2}{x+3} 图像的对称中心坐标。
思路

1.直接代入，简单粗暴
代入几个数值，看一看有没有规律（其实挺适合这道题的，只是不适合我）
第一问代入 x=-4,x=-3,x=0,x=1 ;
你就会发现 f(0)+f(-3)=f(1)+f(-4)=2 。
第二问代入 x=0,x=1,x=2,x=3,x=4 ;
你就会发现f(0)+f(4)=f(1)+f(3)=2f(2)=6 。
缺点：对我这样的非酋太不友好了，别人试了几下就算出来了，可是我可能要试个两三分钟，欸
所以，我要另寻新解法
2.我的解法：构造函数
我构造一个 g(x)=\frac{x}{x+1} ;所以 f(x)=g(x)+g(x+1) ,绘出 g(x) 图象；


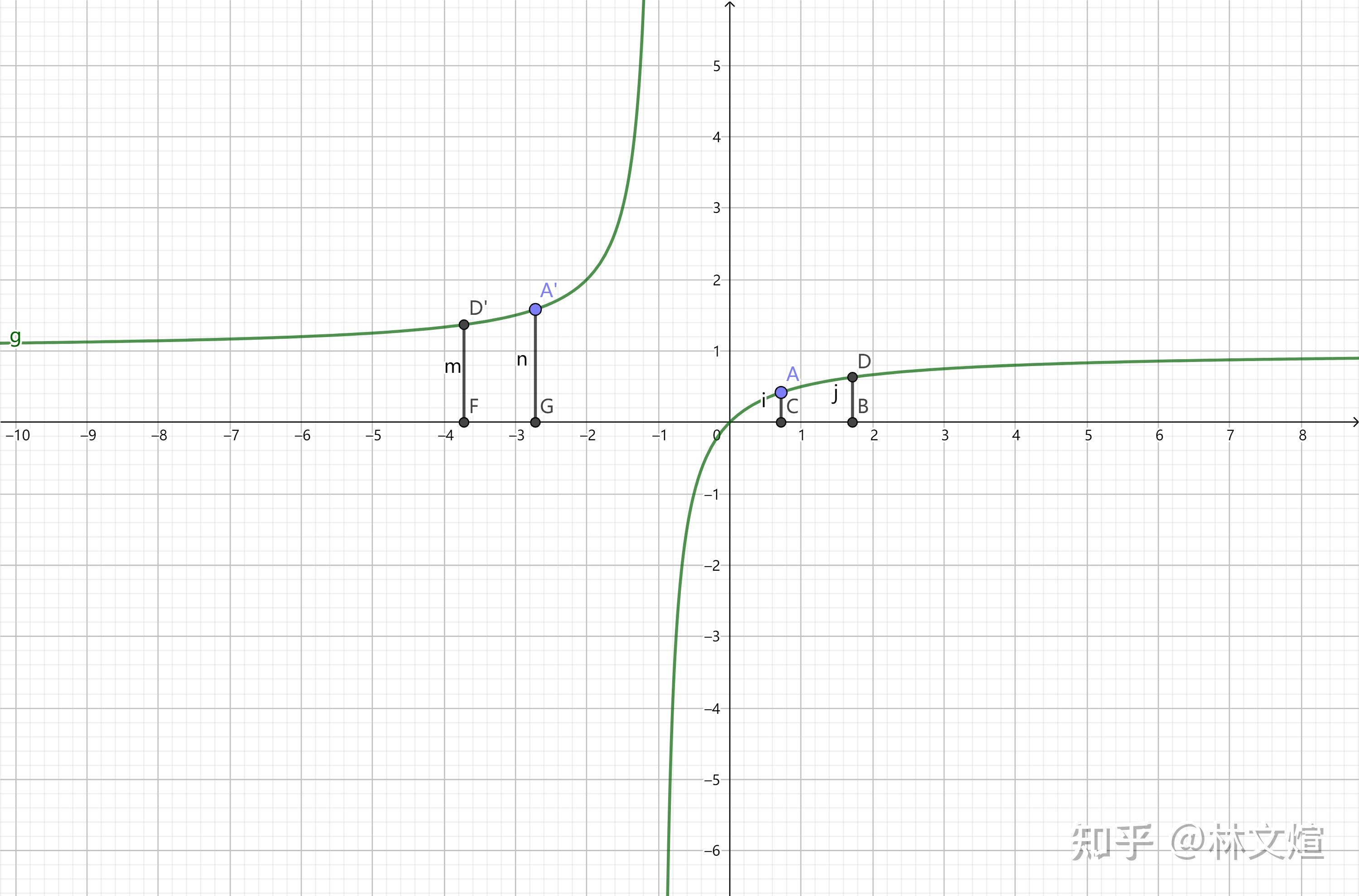
如图，以 x_{A}=x_{C} 为 x ,所以 AC=\frac{x}{x+1} , BD=\frac{x+1}{x+2} ;
由 g(x) 中心对称性质可看出 AC+A'G=DB+D'F ;
也就是 g(-2-x)+g(x)=g(-3-x)+g(x+1)=2 ;
所以 g(x)+g(x+1)+g(-3-x)+g\left((-3-x)+1\right)=4 ;
即 f(x)+f(-3-x)=4 ;
一眼看出 f(x) 关于 (-1.5,2) 对称。
第二题也可以这样解出来关于 （-2，3） 对称。
你以为这就结束了吗，不，没有，看到这道题，我陷入了思考
变式一

是针对这道题的
f_{1}=\frac{x}{x+1}\\ f_{2}=\frac{x}{x+1}+\frac{x+1}{x+2}\\ f_{3}=\frac{x}{x+1}+\frac{x+1}{x+2}+\frac{x+2}{x+3}\\ ……\\ f_{n}=\sum_{i=0}^{n}\frac{x+a_{i}}{x+a_{i+1}}
(知乎级数和极限的排版方式和我看的同济高数不一样，看着好难受)
1.求出函数 f_{a} の对称中心 A(x_{A},y_{A}) 中 x_{A} , y_{A} 关于 a 的函数关系。
2.求出函数 \lim_{n \rightarrow +\infty}{f_{n}} 的对称中心与原点连线与 x 轴夹角。
答案



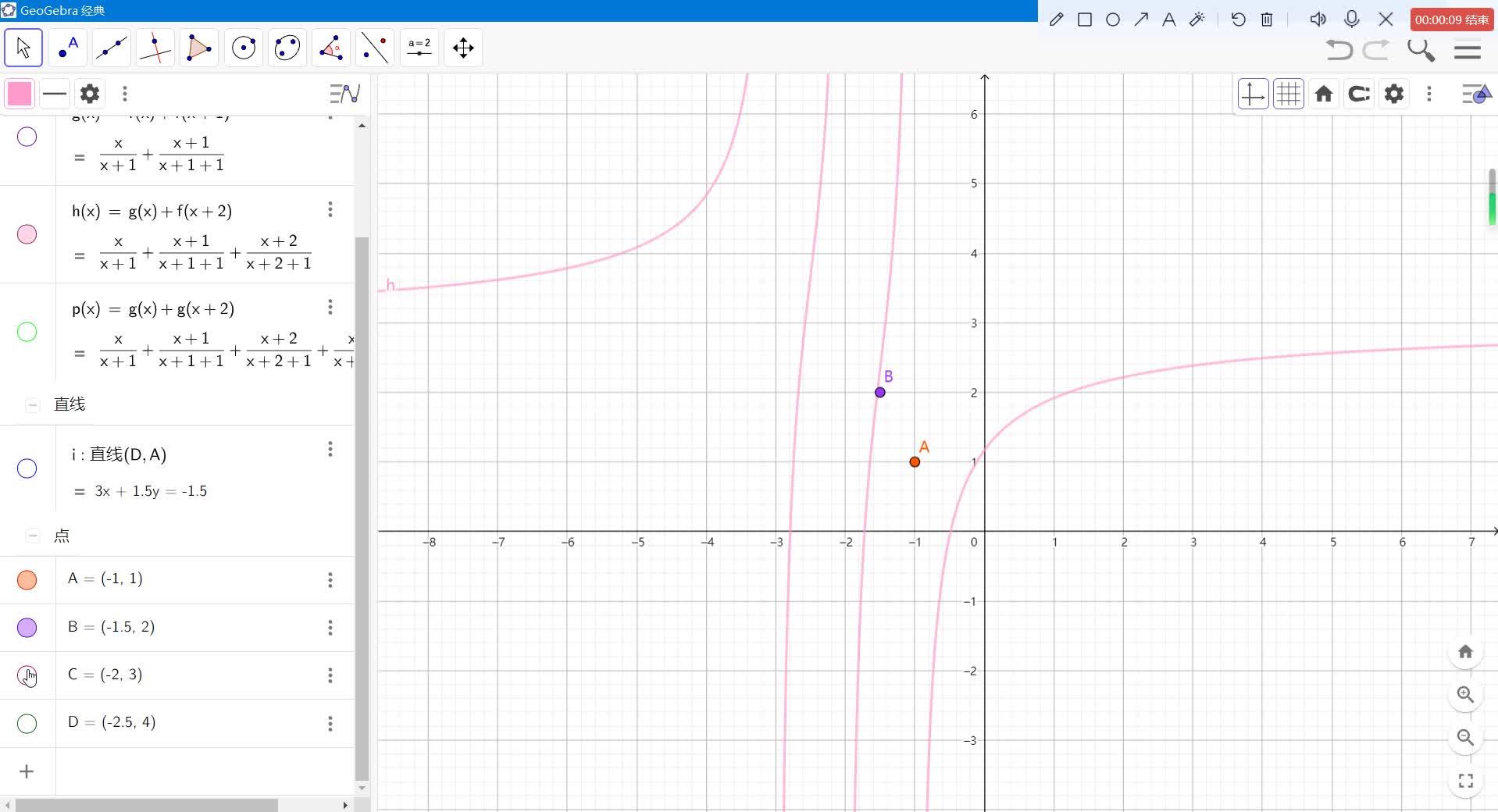
https://www.zhihu.com/video/1592865336856039424
  1.   x_{A}=-0.5a-0.5   ，     y_{A}=a
2. \theta \approx 2.67
<hr/>构造函数练手（应该是高考难度吧）

3.f(x) 定义域在 (0,+\infty) 上，当 x_{2}>x_{1}>0 时， x_{2}f(x_{1})-x_{1}f(x_{2})>x_{2}e^{x_{1}}-x_{1}e^{x_{2}}，f(1)=e+1 ；
解 f(lnx)>lnx+1 。
思路

由 x_{2}f(x_{1})-x_{1}f(x_{2})>x_{2}e^{x_{1}}-x_{1}e^{x_{2}} 移相同除 x_{1}x_{2} ，( x_{1}x_{2}>0 )
得 \frac{f(x_{1})-e^{x_{1}}}{x_{1}}\geq\frac{f(x_{2})-e^{x_{2}}}{x_{2}} ，
正常人一眼就能看出构造 (0,+\infty) 上减函数 g(x)=\frac{f(x)-e^{x}}{x} ，
\because f(1)=e+1  
\therefore g(1)=1
要解 f(lnx)>lnx+1 ,
即解 g(lnx)>1
也就是 g(lnx)>g(1)
x\in(0,e)
证毕
评论

这道题就不能投机取巧代入了，不过也不是太难（我同学给我的题）
<hr/>来个猛的

4.已知a、b、c、d、e\in R 满足
a+b+c+d+e=8\\ a^2+b^2+c^2+d^2+e^2=16
求 e 的最大值
思路

构造 f(x)=(x-a)^2+(x-b)^2+(x-c)^2+(x-d)^2
则 f(x)=4x^2+(a+b+c+d)x-2(a^2+b^2+c^2+d^2)\geq0
即 f(x)=4x^2-2(8-e)x+(16-e^2)\geq0
二次项系数 4>0
\Delta=5e^2-16e\leq0\\ e\in\left(0,\frac{5}{16}\right)
所以 e 的最大值为 \frac{16}{5} 。
<hr/>最后一题？对，是最后一题了

注：这是我自己分析的，可能有许多疏漏，希望热心知友指正。
5.已知函数
f_{1}(x)=cos(x)\\ f_{2}(x)=cos(x)+cos(x+\frac{\pi}{6})\\ f_{3}(x)=cos(x)+cos(x+\frac{\pi}{6})+cos(x+\frac{\pi}{3})\\ f_{4}(x)=cos(x)+cos(x+\frac{\pi}{6})+cos(x+\frac{\pi}{3})+cos(x+\frac{\pi}{2})\\ ……   
（懒得用级数表示了）
1.求出 f_{1}、f_{2}、f_{3}、f_{4}、f_{5}、f_{6}在 y 轴左边第一个最高点坐标。
2.拟合（1）中最高点坐标
分析

作图


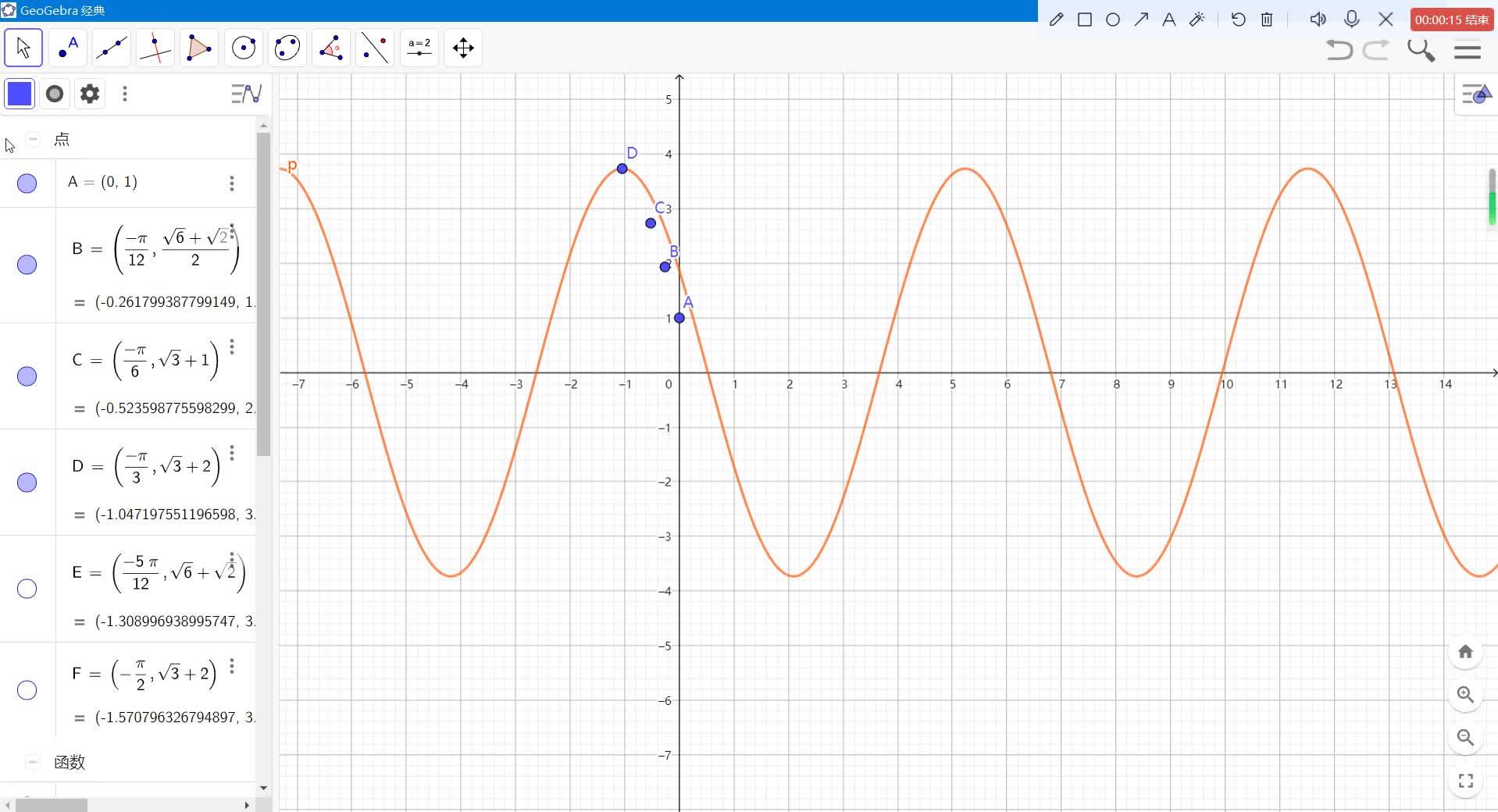
https://www.zhihu.com/video/1592903348721790976
毫无疑问， f_{1} 的最高点为 （0，1） ；
f_{2}(x)=f_{1}(x)+f_{1}(x+\frac{\pi}{6})
也就是 f_{1}(x) 与 f_{1}(x+\frac{\pi}{6}) 和最大的时候 f_{2}(x) 最大，
当 f_{1}(x)=f_{1}(x+\frac{\pi}{6}) 时和最大，
求出 Max\left(f_{2}(x)\right) =f_{2}(-\frac{\pi}{12}) =\frac{\sqrt6+\sqrt2}{2} ,
最高点 \left(-\frac{\pi}{12},\frac{\sqrt6+\sqrt2}{2}\right) ；
别的同理，看上面图中点 A、B、C、D、E、F ；
于是得出 t(x)=-(\sqrt6+\sqrt2) sin\left(x-\frac{π}{12}\right) 。
结语

这篇文章终于结束了，作为一个高中生，我足足花了三天时间整理题目+写了这篇文章。
因为这是我的第一篇文章，难免有许多缺点，后面我也会发一些物理和大学数学学习的文章（毕竟我的目标是物理竞赛），而高中数学类，如果赞同的人数不多，那我可能会弃坑，希望看到的知友点赞鼓励，就算不行，提提建议和意见也可，总之，感谢您的收看。

李老

……

俞瑶

求沙发