|
|
高中的题型中,思维难度最大的是数列和不等式,其次是函数,函数比较活,要靠平时 积累。然而会做高难度题型显然是不够的,很多人栽在时间不够和计算失误上。在高考有限 的时间内能尽可能挤出时间去解决高难度题型是得高分的关键之一。下面推荐几个方法,可 以减少不少运算,而且能有效提高计算准确率。 假如能在高考中节约 10 分钟,那都是异常宝贵的,更不用说提高计算准确率了。
注意:下面这些方法是高中没有讲的,在做题时一定注明用到的定理方法名称。否则遇到钻 牛角尖的改卷老师,只能白吃亏。
一.立体几何
(强烈建议学会这个方法,其他的如果觉得理解困难可以不掌握。)
行列式简化运算(大概减少 5 分钟运算),在涉及法向量的计算时用行列式会非常简洁。
二阶行列式
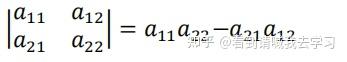
(即对角线乘积之差)
三阶行列式
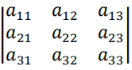
可以按照某一行或者某一列展开(习惯按照行展开)
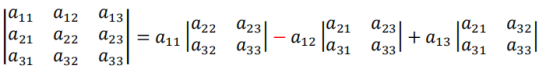
(即某个元素乘以剔除这个元素所在行和列后所得的新行列式,注意第二个展开式前面是负号,这里是最容易错的)
立体几何里要用到向量乘法扩展。
1.求平面法向量
做立体几何的试题的模式化操作无非是建立直角坐标系,然而有点难度的题都会考法向量的 应用,平常解方程组的方法求法向量非常麻烦,还要讨论方向。但用这个方法非常简便,能 节省不少时间。(大一开始就要学这个,其实高中就应该学。) 这是行列式最有用最简洁的地方 。
设方程组求解需要解三元一次方程还要指定一个变量为定值,比较麻烦而且容易出错。
下面的方法简单且容易记忆。
设n是a= (x1, y1, z1),b = (x2, y2, z2)所成的平面的法向量,
则(i,j,k是坐标轴单位向量)
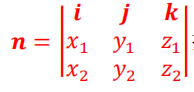
按第一行展开,就求得n的向量表达式
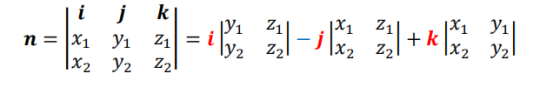
当然,还可以写成更简单的坐标形式。
求出的法向量最好把长度提出来写成单位向量乘以长度,
即
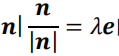
计算时直接算单位向量e要方便得多。因为某向量在单位向量的方向的投影就是a.e。
步骤:
n=行列式 = 行列式展开式 = 坐标式 =λe
顺便说一下

(显然,若n=0,则a,b共线,等效a=λb),n的大小等于a,b所成平行四边形的面积。
(这个就是向量积n=axb,也叫外积,向量积n是一个向量,而且垂直于a,b。物理上的洛伦兹力表达式就是这个关系。
最后关于法向量n的方向:(n=axb)
右手定则:右手除了大拇指的其余四指,指头所指的方向从向量的方向弯向向量的方向, 弯过的角度小于 180 度,大拇指所在方向就是n的方向。
有时候二面角不容易判断是钝角还是锐角,要确定法向量的具体方向,在平面的哪一侧。可见使用向量外积可以直接确定法向量的精确坐标,而设方程还要进行方向的讨论,非常麻烦。
2.求平行六面体体积
假设a=(x1,y1,z1),b=(x2,y2,z2),c=(x3,y3,z3),求a,b,c组成的平行六面体体积v。

(行列式再加绝对值)
(混合积(axb).c,它的大小等于a,b,c组成的平行六面体体积,高中生完全可以推出这个结论。解题时写到混合积……)。
3.求三角形面积
设a=(x1,y1,z1),b=(x2,y2,c2),求a,b所成三角形面积s
因为
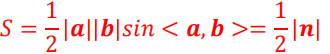
所以按照上面的,先求出n,在算出n的大小,最后除以2。
(上面解题时写到向量积……)
如果是二维(平面)坐标就更加简单了,已知a=(x1,y1),b=(x2,y2),可看作三维坐标下z=0,(axb).(0,0,1)即三角形面积数值上等于高为1 的平行六面体体积的1/2。
即:
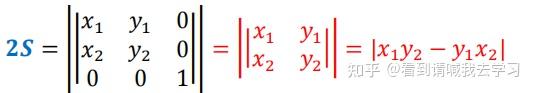
若已知三角形三个顶点坐标,写出 2 个向量,按照这种方法很快就能求解,避免了大量的运算。
这个可转化为求三棱柱体积、三棱锥体积、四棱锥体积。
三棱柱体积等于平行六面体体积的 1/2
三棱锥体积等于平行六面体体积的 1/6(棱锥体积等于相应棱柱体积的 1/3)
四棱锥体积等于平行六面体体积的 1/3
二.解析几何
解析几何的思维难度不大,重点是简化运算。下面给出几个经验公式,能大概简化 3 到 5 分钟运算。高中解析几何一般就涉及直线与圆锥曲线相交问题。
1.抛物线切线
若抛物线是 = ²,则求导求切线更容易。
2.关于何时消x,y
一般来说消 就行了 ,以下几种情况会事半功倍 ,
(1)双曲线、抛物线口朝哪根轴就消那个 ,
这样可以避免直线垂直曲线对称轴时的讨论。
例:抛物线为 ² = 2 ,直线设 = + 最佳(不平行 轴)
(2)直线交坐标轴于 ,与圆锥曲线交于 ( 1, 1) ( 2, 2), 分 的比为 。
若 在 轴上则消
若 在 轴上则消
因为这样,比如:若 在 轴上, 1 = ± 2,简化运算。
3.直线与圆锥曲线交线长度
设直线 = + 与圆锥曲线 ² + ² + + + = 0
消去 后得到 ²+ + =0
一般我们常常会用到
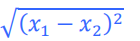
如果按照韦达定理带入表达式计算,那样容易出错。其实很容易证明:
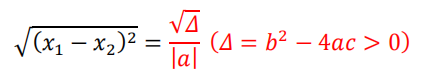
比如,交线长度的经验公式:
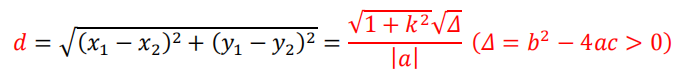
消去 后得到 ² + + = 0
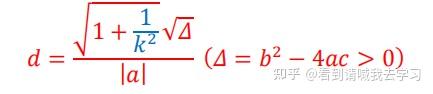
由于是个经验公式,前面最好写上
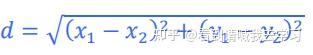
直线设成 = + 时同理,注意此时斜率为:
4.几何性质简化运算或提供思考方向
圆锥曲线的几何性质(第一定义)、三角形的中位线性质……不一一举例。
*我就说一些不常见的,有点难的。关于几个初中定理的反推(这几个定理本来就是充分必要条件,只是在初中只讲充分条件的部分),主要用于提供思考方向,一般对很难的问题来说可能有些帮助。
(1)初中的切割线定理,反之若那种情形的比值条件成立,则相应的直线与圆相切。
(2)初中的圆周角相等定理,反之,即三点,2 定点,1 动点,若动点与而定点所成的角为定值,则这三点在一个圆上,即动点的轨迹是个圆。
三.求极限
求极限的简便方法,我推荐大家最好掌握,万一遇到抽筋的极限可以轻松解决。在一般的不定型极限里也是事半功倍。
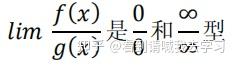
(只有这 2 种时才能用)
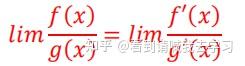
注意:后者无穷时前者也无穷,后者摆动时前者可能还存在极限。
例:
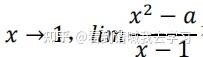
有极限,求这个极限。
一般的做法要求出 ,而这个做法就可以绕过它。
上下分别求导得:
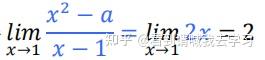
当然这是小儿科级别,对于一般难求的极限,这个法则的作用就大了,求导一般来说可以降 次,从而有效简化运算。 注意:解大题时写上由洛必达法则……
四.求导
求导有比较多的简化方法。其中只说隐函数求导法则,一个函数,例如抛物线: 2 = 2 ( > 0),也可以写成 = √2 。
前者就是隐函数,后者就是显函数。 是一个关于 的函数,由复合函数求导法则知,所以对 ( )求导 ′ ( ) ′ 。
两边求导:
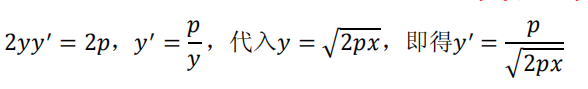
如果对于关系复杂的显函数求导,比如:
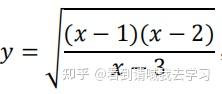
求导比较痛苦。然而如果我们用隐函数求导法则,两边取对数:
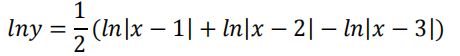
两边求导:
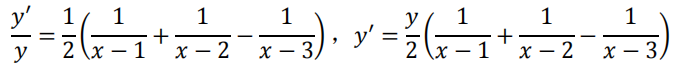
代入:
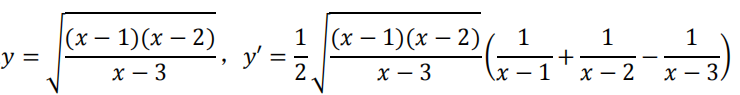
上面类似的根式形式都可以用这个做法。 这个东西考得比较少,可以不掌握。但建议掌握隐函数求导法则,在解某些物理题时,隐函数数求导是事半功倍的。
当然了,如果想要更进一步可以去购买一些感兴趣的课程或者书籍,自我进修。 |
|